Numerical modeling of the field-induced deformation and the corresponding optical properties
 The orientation of the director (local optic axis) inside the LC-layer as a function of the position is described by the director field. Oseen, Frank, Leslie, Ericksen, and others developed the theory of LC elasticity which is used in DIMOS for calculation of the director orientation within the bulk of chiral-nematic LC-materials. This model covers the static and dynamic case including flow effects and elastic boundary coupling.
The orientation of the director (local optic axis) inside the LC-layer as a function of the position is described by the director field. Oseen, Frank, Leslie, Ericksen, and others developed the theory of LC elasticity which is used in DIMOS for calculation of the director orientation within the bulk of chiral-nematic LC-materials. This model covers the static and dynamic case including flow effects and elastic boundary coupling.
Stepping towards stable solutions is achieved by suitable relaxation methods which also allow the simulation of the time dependent behavior in a natural way by use of dissipation functions which are based on the viscosities of the LC material. Thus the director dynamics are computed on a physical time scale.
DIMOS optical workbench
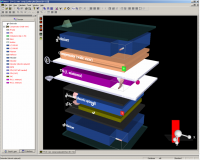
This stack editor is provided in DIMOS for easy and convenient definition of stacks of optical layers via drag and drop of various components. Light sources, filter wheels, observers and filters complete the optical bench of DIMOS.
Material-Property Editor
DIMOS distinguishes the following media:
- Chiral nematic (cholesteric) Liquid crystalline medium with anisotropic elastic, dielectric, flexoelectric, and optical properties,
- isotropic dielectrics (i.e. glass, polyimide, etc.) described by their dielectric constants and refractive index,
- uniaxial and biaxial solids (i.e. retarder sheets).
Database
DIMOS comprises a specially developed database system, which enables easy administration of the complex material, layer and model descriptions and supports multi-user administration by a versatile user/rights management concept.
Results
The results of the calculations can be represented in various graphical forms:
- static and dynamic director orientation in chiral-nematic liquid crystals in one dimension (tilt and twist profiles, molecular plots, paths on geodesic surface, etc.),
- intensity of transmittance and reflectance versus direction of light propagation (viewing direction) in polar coordinate systems, state of polarization, transfer matrix elements, etc.),
- variation of chromaticity coordinates in various systems of the CIE (e.g. CIE 1931, CIE 1976, etc.) versus arbitrary variables.